Table of Contents
Introduction
Category Theory is a mathematical discipline with a wide range of applications in theoretical computer science. Concepts like Category, Functor, Monad, and others, which were originally defined in Category Theory, have become pivotal for the understanding of modern Functional Programming (FP) languages and paradigms. The meaning and applications of these terms in FP can be understood without in-depth knowledge of the corresponding mathematical definitions and axiomatic. However, a common knowledge of the underlying theory can help FP programmers understand the design and structure of commonly used libraries and tools and be more productive.
This series of tutorials defines and illustrates the Category Theory concepts which are most widely adopted in FP. We will use simple Scala and pseudocode examples to illustrate the new terms.
Categories
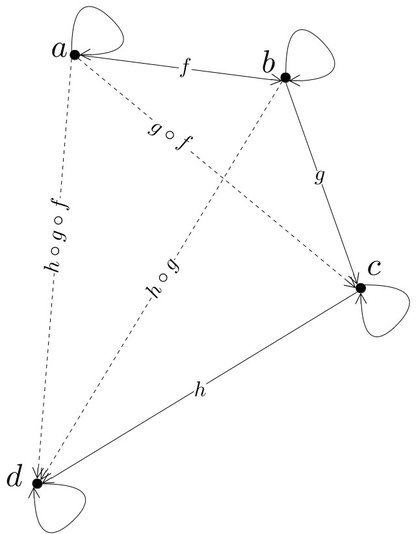
A category is a simple algebraic structure for modelling objects and their relationships. A category C consists of a collection of objects ob(C) and a collection of arrows/morphisms hom(C) connecting the objects. In other words, every arrow f can be defined as a pair [a,b] of the objects it connects. We write f: a → b.
A category also defines an operation for composing arrows, such that for every f: a → b and g : b → c, their composition g ∘ f is also an arrow, which connects a and c - i.e. g ∘ f: a → c.
A collection of objects and arrows qualifies as a category only if:
- The composition is associative. More formally, h ∘ (g ∘ f) = (h ∘ g) ∘ f for every three arrows, and;
- For every object a there is an identity arrow (i.e. a loop) ia that connects it to itself: ia: a → a.
- The identities should have the obvious property that for every f: a → b the following is true ib ∘ f = f = f ∘ ia. In other words, identities are neutral to composition.
Examples
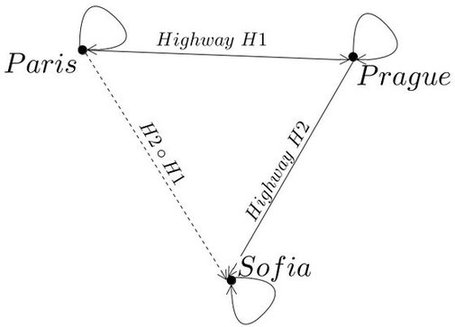
An intuitive example of a category is the inter-city road infrastructure. A portion of this category is depicted in the diagram below. In it, the objects are all cities around the world. We consider two cities to be connected with an arrow if one is reachable from the other. We assume each city is reachable from itself which is represented with the identity arrows. If we can travel from city A to B, and from B to C, then we can do so from A to C. Hence, we can compose arrows.
More generally, every directed graph forms a category whose objects are the graph nodes. In it, two nodes/objects a and b are connected with an arrow only if there is path between them in the graph. We also consider that every node in the graph has an arrow to itself - i.e. it is reachable from itself.
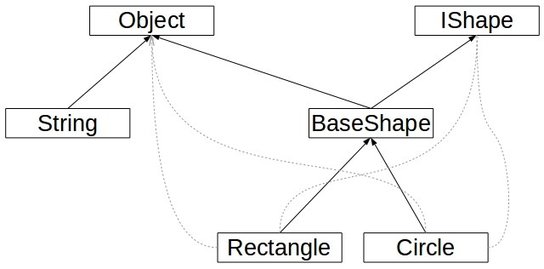
In Object Oriented Programming (OOP), a class hierarchy also forms a category. The category objecta are the types (e.g. classes, traits, interfaces). We consider two types A and B to be connected with an arrow if A is a subtype of B. These arrows are composable, because if A is a subtype of B, and B of C, then A is a subtype of C. Finally, each type is a subtype of itself and thus we have identity arrows as well. This is depicted in the following figure.
The Hask Category
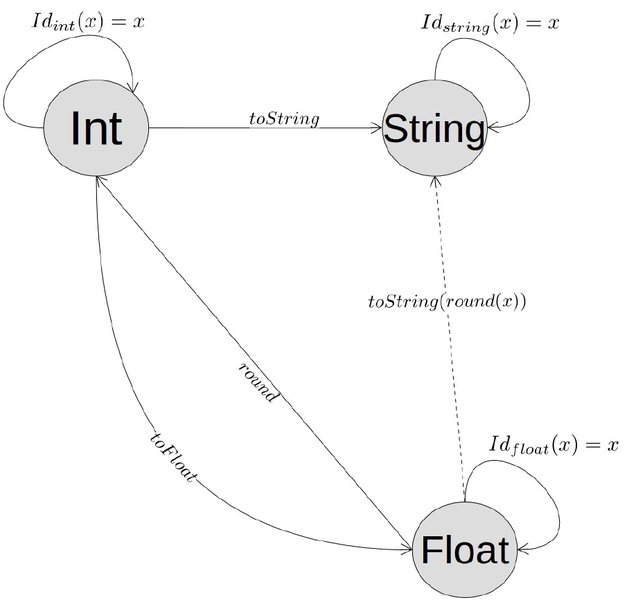
In Functional Programming, the Hask category has a special role. The objects of Hask are all types of the Haskel programming language - i.e. Ob(Hask) = {Int, String, …}. We can generalise that to the types of other languages, like Scala, as well. For every function converting one type to another, in Hask there is an arrow between the two types. Arrow composition is just function composition. The identity arrows correspond to the identity functions. The following diagram depicts a portion of the Hask category.
Functors
In category theory, a Functor F is a transformation between two categories A and B. We write F : A → B. F must map every object and arrow from A to B. In other words, if a ∈ ob(A) then F(a) ∈ ob(B), and if f ∈ Hom(A) then F(f) ∈ Hom(B).
We also require that F preserves the structure (i.e. identity arrows and composition) of the source category. More formally:
- If f : a → b is an arrow in A then F(f):F(a) → F(B) is an arrow in B.
- F(idX) = id(F(X)), which means that each identity arrow in A is transformed to an identity arrow of the corresponding object in B.
- F(g ∘ f) = F(g) ∘ F(f), which means that the mapping of arrows’ composition in A is a composition of their mappings in B.
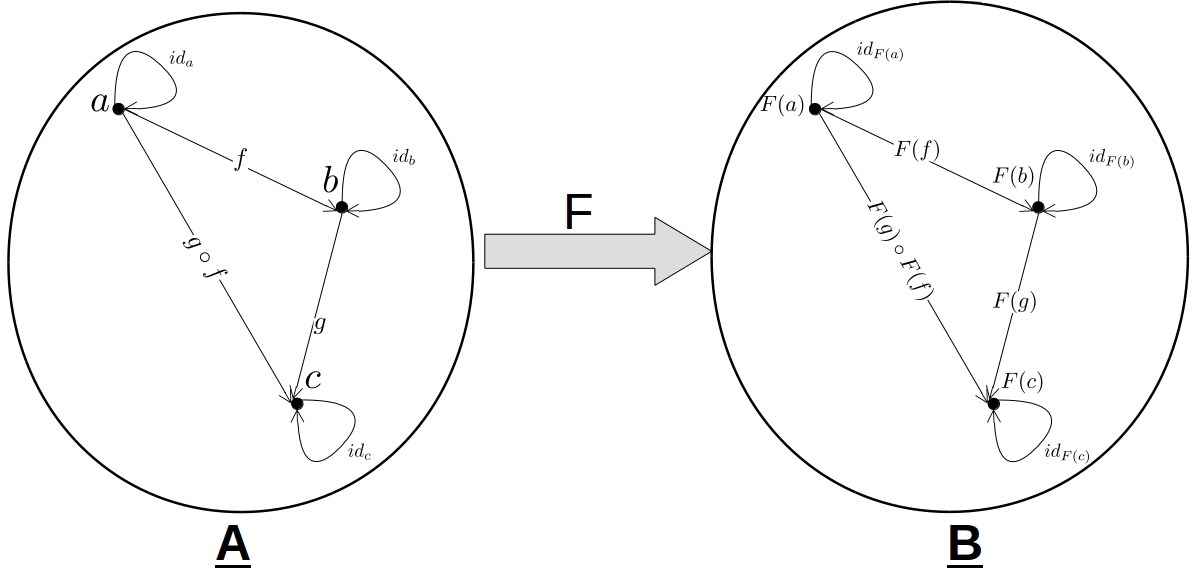
When a functor F transforms a category A into itself, we call it an endofunctor and we write F:A → A.
Functors in FP
Before we delve into Functors and FP, we need to introduce the concept of a type constructor. Essentially, a type constructor is a generic type definition, which takes another type as a parameter. For example, in Scala List[T], Vector[T], and Option[T] are type constructor. You need to specify the value of the type parameter T in order to produce a concrete type. For example, List[String] is a type, while List itself is not - it is a type constructor. We will write TC[ _ ] to denote that TC is a type constructor.
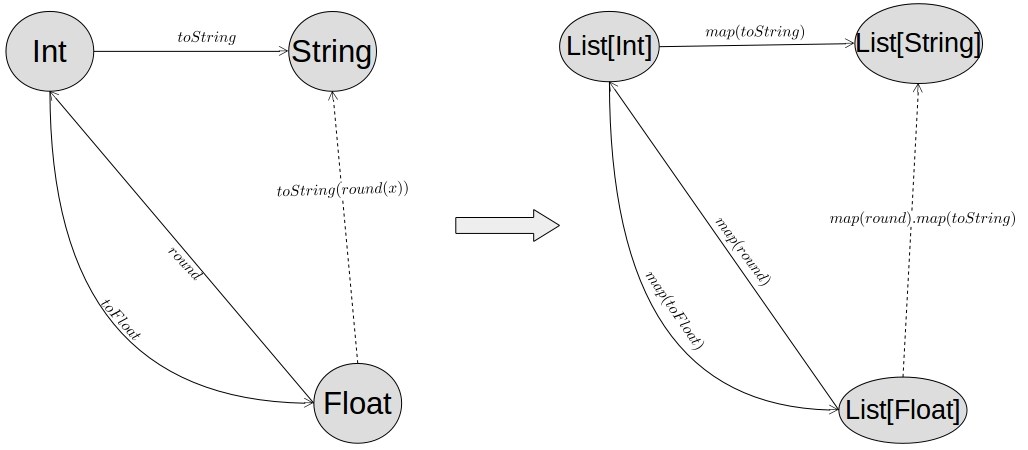
Functors in Category Theory are a much more general concept than in functional programming (FP). All functors in FP are just endofunctors in Hask. Furthermore, each functor F is associated with a type constructor TC[ _ ]. Each type A in Hask is transformed to TC[A]. For example, if TC = List then F: Int → List[Int]. In other words, the type constructor uniquely defines the mapping of Hask objects.
In order to define a functor, we also need to define the arrow mapping. The arrows in Hask are just functions. Hence, we need to provide a function called map with the following signature: map: (A → B) → (TC[A] → TC[B]). For every arrow/function f: A → B it returns its projection/mapping which is also a function - F(f): TC[A] → TC[B].
To summarise, a functor in FP is uniquely defined by a type constructor TC[ _ ] and a map function with the aforementioned signature. The following diagram depicts a functor, whose type constructor is List[_].
Functors in code
Following the previous definitions, in Scala a functor can be defined as:
1
2
3
trait Functor[TC[_]] {
def map[A,B] (f: A => B): (TC[A] => TC[B])
}
Note that the return type of map is a function. Often the caller just wants to apply/run this function to a given arguement, instead of passing it on as an arguement or reusing it later on. Thus, it is convenient to use another analogous definition of a functor, which also applies the resulting function:
1
2
3
trait Functor[TC[_]] {
def map[A,B] (f: A => B)(param : TC[A]) : TC[B]
}
This is essentially a shortcut for mapping a function and applying it in one go. We can also define the map function as a method of the type constructor TC itself:
1
2
3
trait TC[A] {
def map[B] (f: A => B): TC[B]
}
For simplicity, in this case we can just say that TC itself is a functor, because it is a type constructor and has a map function. To make it more readable we can just write:
1
2
3
trait Functor[A] {
def map[B] (f: A => B): Functor[B]
}
This trait can then be implemented from all concrete type constructors (e.g. List and Vector) thus making them functors.
Examples
In FP, functors are usually applied to map/convert instances of generic data structures (i.e. type constructors) in a way which preserves their inner structure. For collections like List and Vector we would implement the map function by just applying it to every element, as in the following pseudocode:
1
2
3
4
5
6
7
8
9
10
class List[A] extends Functor[A] {
// ...
def map[B] (f: A => B): List[B] = {
this match {
case List() => this
case h::t => f(h)::(t.map(f))
}
}
// ...
}
For type constructors which encode “success-or-failure” state like Option or Either the map function can be applied only if there is a contained value:
1
2
3
4
5
6
7
8
9
10
class Option[A] extends Functor[A] {
// ...
def map[B] (f: A => B): Option[B] = {
this match {
case None => None
case Some(x) => Some(f(x))
}
}
// ...
}
Given that all these functors have a common supertype allows us to write functions which will work with all of them. For example:
1
2
def useAnyIntFunctor(functor: Functor[Int]) =
functor.map(_ + 5).map(_ * 2)
This will work “as expected” with all functors - Option, List, etc. However, in this example the return type is Functor, not the actual compile-time type of the parameter. This can be amended by defining a method type parameter for the arguement’s type.
Update: updated with comments from Ken Scambler and other collegues from REA

