Curried Functions

Before we discuss applicative functors, we need to introduce the concept of currying. In FP, we can partially apply a function of multiple parameters by specifying a subset of its required parameters. For this purpose, Scala offers special syntax, allowing us to group function parameters into separate parameter lists.

1
2
3
4
5
6
7
def curriedF(x : Int) (y : Int) = x + y

// We need to use underscore after the function invocation
val partiallyApplied : Int => Int = curriedF(1)_

// Call the partially applied function. Result is 3
val result = partiallyApplied(2)

The ability to create partially applied functions is called currying. Scala also allows us to create curried functions from non-curried ones:

1
2
3
4
5
6
7
8
9
// Non-curried
def f(x : Int, y : Int) = x + y

// Make a curried version of f
val fCurried = (f _).curried

// Invoke the non-curried and curried functions
f(1, 2)
fCurried(1)(2)

In fact, this is a much more general idea which is not specific to Scala and FP. Unfortunately, most languages do not explicitly support currying. We can still easily curry every function in most modern languages as long as they support anonymous functions, as in the following Python example:

1
2
3
4
5
6
7
8
9
# Non-curried
def f(x, y): return x + y

# Make a curried version of f
def fCurried(x): return lambda y : f(x, y) 

# Invoke the non-curried and curried functions
f(1, 2)
fCurried(1)(2)

Curried and non-curried functions are equivalent. As we just showed, we can convert each function to a curried one. The opposite is also true. In terms of notation, we’ll denote the non-curried version of a function as f: (A₁ × A₂ × … × A_n-1) → A_n, or we could just write: f: (A₁, A₂, …,A_n-1) → A_n.

The curried version will be written as: f: A₁ → A₂ → … → A_n.

Currying is a simple but powerful method to represent a function with multiple arguements as a single-arg function. This allows us to generalise everything that works for single arguement functions to the multi-arguement case.

Applicative Functor: Structure and Computation

An applicative functor is defined by:

• A type constructor F[ _ ] - e.g. List, Option;
• A function pure : A → F[A], where A can be any type (including types of functions);
• A function apply: F[A → B] → (F[A] → F[B]), where A and B can be any types (including types of functions);

Function “Pure”

The pure function is also known as point in some languages and libraries. Essentially, it is a constructor which can convert a value of any type A to a value of F[A]. We often say that pure “lifts” its arguement to the corresponding type defined by the type constructor (e.g. from Int to List[Int]). Here is a sample implementation for Option.

1
2
3
4
5
6
7
// Implementation for Options
def pure[A](a : A) : Option[A] = Some(a)

pure("Text") // Some("Text")

// We can also embed a function in an Option
pure(x:Int => x.toString) //Some(Int => String)

Similarly, an implementation of pure for List would just wrap it in a list:

1
2
3
4
5
// Implementation for List
def pure[A](a : A) : List[A] = List(a)

// We can embed a function in a list
pure(x:Int => x + 1) //List(Int => Int)

Function “Apply”

The apply function takes a function, which is embedded into the context defined by the type constructor (e.g. Option[A → B]), and lifts/converts it to a function in the realm of the type constructor (e.g. Option[A] → Option[B]). Here is a sample implementation for Option:

1
2
3
4
5
6
7
8
  // Implementation for Option
  def apply[A, B](oFunc : Option[A => B]) : Option[A] => Option[B] = {
    // Returns an anonymous function
    oA: Option[A] => oA match {
      case None => None
      case Some(a) => oFunc.map(f => f(a))
    }
  }

Implementing “apply” for List is somewhat less straigthforward. Given a list of functions (i.e. List[A → B]), we need to return a function that converts from one list to another (i.e. List[A] → List[B]). One approach is to return a function, which applies all functions in the given list to all elements in its input parameter:

1
2
3
4
5
6
7
8
9
10
11
  // Implementation for List
  def apply[A, B](lFunc : List[A => B]) : List[A] => List[B] = {
    // Create an inner result function
    def resultF (lA: List[A]) : List[B] = {
      lA match {
        case List() => List()
        case head :: tail => lFunc.map(f => f(head)) ::: resultF(tail)
      }
    }
    return resultF
  }

Variations

The apply function returns a function as a result. One would usually take this result and invoke it with some parameter. Hence, it often makes sense to use an alternative signature for the apply function:

1
def apply[A,B](f: F[A=>B], fa: F[A]): F[B]

This definition does both at the same time - it converts/maps the lifted function f: F[A=>B] to a function of type F[A]=>F[B] and then applies it to the second arguement fa. It is a convenience “wrapper” for the previous definition of apply. In the rest of the article we’ll use both definitions interchangeably in accordance with the needs of each example.

Putting the Pieces Together

Let’s consider a multi-argument curried function f: A₁ → A₂ → … → A_n. The function pure can embed f into an instance of F[A₁ → A₂ → … → A_N].

This sets the stage for an invocation of the apply function which transforms F[A₁ → A₂ → … → A_N] to F[A₁] → F[A₂ → … → A_N]. We can further use apply repeatedly to transform this to F[A₁] → F[A₂] → … → F[A_N], and hence we have been able to “lift” the f function into the applicative functor. This computation is depicted in the next figure.

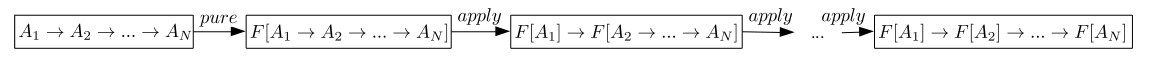
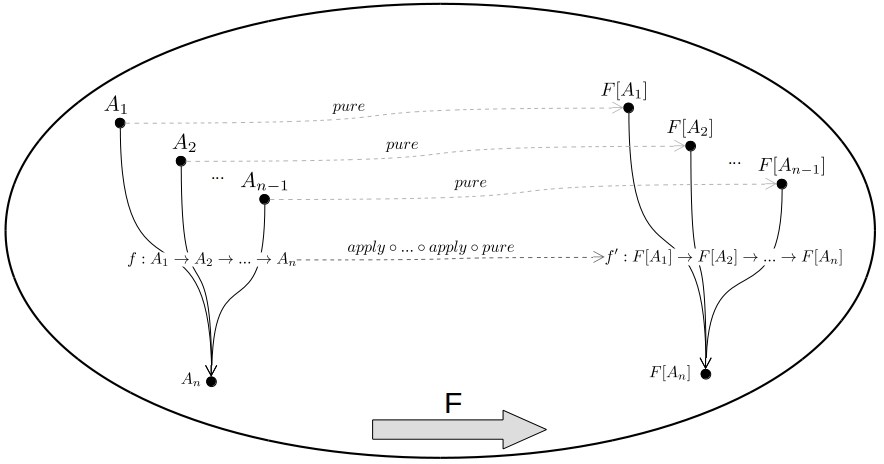
The following diagram depicts how an Applicative Functor acts as an endofunctor in the Hask category. It shows how the generic function pure maps each type (i.e A₁ … A_n) to the corresponding type defined by the type constructor (i.e F[A₁] … F[A_n]). By composing the apply and pure functions, we can map any function f: A₁ → … → A_n to a function with the following form f ‘: F[A₁] → … → F[A_n].

Going back to the example from the motivation section, we can implement the desired logic as:

1
2
3
4
5
6
def sum(x : Int)(y : Int) = x + y
val xOpt : Option[Int] = Some(1)
val yOpt : Option[Int] = Some(2)

// The result is Some(3)
apply(apply(pure(sum), xOpt), yOpt)

For convenience, some languages and libraries alias the apply function with the left associative <*> operator, which allows for the more succinct expression:

1
pure(sum) <*> xOpt <*> yOpt

Laws

This section is a bit less intuitive and you may wish to skip it when reading for the first time. To qualify as an Applicative Functor, a pair of apply and pure functions must obey several laws. In this section, we’ll formulate and demonstrate them using the aforementioned Applicative Functor for Option.

Identity Law

The identity law states that pure(id) <*> v = v for every v, where id is an identity function. This rule implies that pure preserves the identity function. The following snippet exemplifies this law for the Option’s applicative functor:

1
2
3
4
5
6
7
8
9
// Identity Function
def id[A](a: A) = a

// Any v - for example Some(42)
val v: Option[Int] = Some(42)

// The following should be true for every v. In other words,
// pure(id[Int]) should be an identity with respect to <*>.
pure(id[Int]) <*> v == v

Composition Law

The composition law states that pure(f) <*> pure(x)=pure(f(x)) meaning that for every function f and value x, applying the lifted/mapped function to the lifted value is the same as lifting the function’s result, as in the following snippet:

1
2
3
4
5
6
7
8
9
// Any function f. For example: x+1
def f(x: Int) = x + 1

// Any x - for example Some(42)
val x: Option[Int] = Some(42)

// The following should be true for every f and x. In other words, "lifting" 
// f and applying x, should be the same as lifting f(x)
pure(f) <*> x == pure(f(x))

Homomorphism Law

The homomorphism law states that pure(∘) <*> u <*> v <*> w = u <*> (v <*> w). Here, “∘” is function composition, which is a function of two arguements (the functions it composes). This law states that function composition is preserved by the applicative functor. The following snippet illustrates:

1
2
3
4
5
6
7
8
9
10
11
12
13
14
// Composition Function
def compose[A,B,C](f: A=>B, g: B=>C) = 
  a: A => g(f(a))

// Any two functions u and v. For example:
def u(x: Int) = x+1
def v(x: Int) = x+2

// Any w - for example Some(42)
val w: Option[Int] = Some(42)

// The following should be true. In other words, pure(compose) 
// should compose u and v with respect to <*>.
pure(compose) <*> u <*> v <*> w == u <*> (v <*> w)

Interchange Law

The interchange law states that u <*> pure x = pure (f => f(x)) <*> u. Therefore, we should be able to change the order of apply’s the parameters. To do so, however, we need to convert the second parameter to a higher order function, as in the following snippet:

1
2
3
4
5
6
7
8
9
// Any function u. For example: x+1
def u(x: Int) = x + 1

// Any u - for example Some(42)
val x: Option[Int] = Some(42)

// The following should be true. In the following code, f is an anonymous
// higher order function that applies its arguement (a function) to x.
u <*> x == pure(f:(Option[Int] => Option[Int]) => f(x)) <*> u

Applicative Functors are Functors

So far we have defined an applicative functor, as a pair of two functions - pure and apply. However, we have not yet shown that it is indeed a type of functor. We can do so by implementing a map function as follows:

1
2
def map[F[]]map(f: A => B, fa:F[A]) =
	pure(f) <*> fa

The previous laws ensure that this implementation conforms to the functor laws.

In the previous post we saw that a Functor can be defined as a trait representing the type constructor and defining the map function as a method. Analogously, we can define the AppFunctor trait as follows:

1
2
3
4
5
6
7
8
9
10
11
12
trait AppFunctor[A] {
    def pure(a: A): AppFunctor[A]

    // OOP version of apply[A,B](f: AppFunctor[A => B], fa: AppFunctor[A]): AppFunctor[B] 
    // We'll use "this" instead of the second parameter "fa".
    def apply[A,B](f: AppFunctor[A => B]): AppFunctor[B] 

    // We can also implement map (from the definition of a Functor) 
    // through the other two methods:
    def map[A,B](f: A => B): AppFunctor[B] =
        apply(pure(f))
}

References

• https://github.com/dcapwell/scala-tour/blob/master/Applicative%20Functor.md
• https://drboolean.gitbooks.io/mostly-adequate-guide/content/ch10.html
• http://808fabrik.com/scala/functor-monad-in-scala-handout.pdf